Flix

GitHub: github.com/okalachev/flix.
Telegram-канал: @opensourcequadcopter.
Архитектура прошивки
Прошивка Flix это обычный скетч Arduino, реализованный в однопоточном стиле. Код инициализации находится в функции setup(), а главный цикл — в функции loop(). Скетч состоит из нескольких файлов, каждый из которых отвечает за определенную подсистему.
Главный цикл loop() работает на частоте 1000 Гц. Передача данных между подсистемами происходит через глобальные переменные:
t(float) — текущее время шага, с.dt(float) — дельта времени между текущим и предыдущим шагами, с.gyro(Vector) — данные с гироскопа, рад/с.acc(Vector) — данные с акселерометра, м/с2.rates(Vector) — отфильтрованные угловые скорости, рад/с.attitude(Quaternion) — оценка ориентации (положения) дрона.controlRoll,controlPitch,controlYaw,controlThrottle,controlMode(float) — команды управления от пилота, в диапазоне [-1, 1].motors(float[4]) — выходные сигналы на моторы, в диапазоне [0, 1].
Исходные файлы
Исходные файлы прошивки находятся в директории flix. Основные файлы:
flix.ino— основной файл Arduino-скетча. Определяет некоторые глобальные переменные и главный цикл.imu.ino— чтение данных с датчика IMU (гироскоп и акселерометр), калибровка IMU.rc.ino— чтение данных с RC-приемника, калибровка RC.estimate.ino— оценка ориентации дрона, комплементарный фильтр.control.ino— подсистема управления, трехмерный двухуровневый каскадный ПИД-регулятор.motors.ino— выход PWM на моторы.mavlink.ino— взаимодействие с QGroundControl или pyflix через протокол MAVLink.
Вспомогательные файлы:
vector.h,quaternion.h— библиотеки векторов и кватернионов.pid.h— ПИД-регулятор.lpf.h— фильтр нижних частот.
Подсистема управления
Состояние органов управления обрабатывается в функции interpretControls() и преобразуется в команду управления, которая включает следующее:
attitudeTarget(Quaternion) — целевая ориентация дрона.ratesTarget(Vector) — целевые угловые скорости, рад/с.ratesExtra(Vector) — дополнительные (feed-forward) угловые скорости, для управления рысканием в режиме STAB, рад/с.torqueTarget(Vector) — целевой крутящий момент, диапазон [-1, 1].thrustTarget(float) — целевая общая тяга, диапазон [0, 1].
Команда управления обрабатывается в функциях controlAttitude(), controlRates(), controlTorque(). Если значение одной из переменных установлено в NAN, то соответствующая функция пропускается.
Состояние armed хранится в переменной armed, а текущий режим — в переменной mode.
Вектор, кватернион
В алгоритме управления квадрокоптером широко применяются геометрические (и алгебраические) объекты, такие как векторы и кватернионы. Они позволяют упростить математические вычисления и улучшить читаемость кода. В этой главе мы рассмотрим именно те геометрические объекты, которые используются в алгоритме управления квадрокоптером Flix, причем акцент будет сделан на практических аспектах их использования.
Система координат
Оси координат
Для работы с объектами в трехмерном пространстве необходимо определить систему координат. Как известно, система координат задается тремя взаимно перпендикулярными осями, которые обозначаются как X, Y и Z. Порядок обозначения этих осей зависит от того, какую систему координат мы выбрали — левую или правую:
| Левая система координат | Правая система координат |
|---|---|
В Flix для всех математических расчетов используется правая система координат, что является стандартом в робототехнике и авиации.
Также необходимо выбрать направление осей — в Flix они выбраны в соответствии со стандартом REP-103. Для величин, заданных в подвижной системе координат, связанной с корпусом дрона, применяется порядок FLU:
- ось X — направлена вперед;
- ось Y — направлена влево;
- ось Z — направлена вверх.
Для величин, заданных в мировой системе координат (относительно фиксированной точки в пространстве) — ENU:
- ось X — направлена на восток (условный);
- ось Y — направлена на север (условный);
- ось Z — направлена вверх.
Углы и угловые скорости определяются в соответствии с правилами математики: значения увеличиваются против часовой стрелки, если смотреть в сторону начала координат. Общий вид системы координат:
Вектор
vector.h.Вектор — простой геометрический объект, который содержит три значения, соответствующие координатам X, Y и Z. Эти значения называются компонентами вектора. Вектор может описывать точку в пространстве, направление или ось вращения, скорость, ускорение, угловые скорости и другие физические величины. В Flix векторы задаются объектами Vector из библиотеки vector.h:
Vector v(1, 2, 3);
v.x = 5;
v.y = 10;
v.z = 15;
vector и динамический массив в стандартной библиотеке C++ — std::vector.В прошивке в виде векторов представлены, например:
accсобственное ускорение с акселерометра.gyro— угловые скорости с гироскопа.rates— рассчитанная угловая скорость дрона.accBias,accScale,gyroBias— параметры калибровки IMU.
Операции с векторами
Длина вектора рассчитывается при помощи теоремы Пифагора; в прошивке используется метод norm():
Vector v(3, 4, 5);
float length = v.norm(); // 7.071
Любой вектор можно привести к единичному вектору (сохранить направление, но сделать длину равной 1) при помощи метода normalize():
Vector v(3, 4, 5);
v.normalize(); // 0.424, 0.566, 0.707
Сложение и вычитание векторов реализуется через простое покомпонентное сложение и вычитание. Геометрически сумма векторов представляет собой вектор, который соединяет начало первого вектора с концом второго. Разность векторов представляет собой вектор, который соединяет конец первого вектора с концом второго. Это удобно для расчета относительных позиций, суммарных скоростей и решения других задач. В коде эти операции интуитивно понятны:
Vector a(1, 2, 3);
Vector b(4, 5, 6);
Vector sum = a + b; // 5, 7, 9
Vector diff = a - b; // -3, -3, -3
Операция умножения на число n увеличивает (или уменьшает) длину вектора в n раз (сохраняя направление):
Vector a(1, 2, 3);
Vector b = a * 2; // 2, 4, 6
В некоторых случаях полезна операция покомпонентного умножения (или деления) векторов. Например, для применения коэффициентов калибровки к данным с IMU. В разных библиотеках эта операция обозначается по разному, но в библиотеке vector.h используется простые знаки * и /:
acc = acc / accScale;
Угол между векторами можно найти при помощи статического метода Vector::angleBetween():
Vector a(1, 0, 0);
Vector b(0, 1, 0);
float angle = Vector::angleBetween(a, b); // 1.57 (90 градусов)
Скалярное произведение
Скалярное произведение векторов (dot product) — это произведение длин двух векторов на косинус угла между ними. В математике оно обозначается знаком · или слитным написанием векторов. Интуитивно, результат скалярного произведения показывает, насколько два вектора сонаправлены.
В Flix используется статический метод Vector::dot():
Vector a(1, 2, 3);
Vector b(4, 5, 6);
float dotProduct = Vector::dot(a, b); // 32
Операция скалярного произведения может помочь, например, при расчете проекции одного вектора на другой.
Векторное произведение
Векторное произведение (cross product) позволяет найти вектор, перпендикулярный двум другим векторам. В математике оно обозначается знаком ×, а в прошивке используется статический метод Vector::cross():
Vector a(1, 2, 3);
Vector b(4, 5, 6);
Vector crossProduct = Vector::cross(a, b); // -3, 6, -3
Кватернион
Ориентация в трехмерном пространстве
В отличие от позиции и скорости, у ориентации в трехмерном пространстве нет универсального для всех случаев способа представления. В зависимости от задачи ориентация может быть представлена в виде углов Эйлера, матрицы поворота, вектора вращения или кватерниона. Рассмотрим используемые в полетной прошивке способы представления ориентации.
Углы Эйлера
Углы Эйлера — крен, тангаж и рыскание — это наиболее «естественный» для человека способ представления ориентации. Они описывают последовательные вращения объекта вокруг трех осей координат.
В прошивке углы Эйлера сохраняются в обычный объект Vector (хоть и, строго говоря, не являются вектором):
- Угол по крену (roll) —
vector.x. - Угол по тангажу (pitch) —
vector.y. - Угол по рысканию (yaw) —
vector.z.
Особенности углов Эйлера:
- Углы Эйлера зависят от порядка применения вращений, то есть существует 6 типов углов Эйлера. Порядок вращений, принятый в Flix (и в роботехнике в целом) — рыскание, тангаж, крен (ZYX).
- Для некоторых ориентаций углы Эйлера «вырождаются». Так, если объект «смотрит» строго вниз, то угол по рысканию и угол по крену становятся неразличимыми. Эта ситуация называется gimbal lock — потеря одной степени свободы.
Ввиду этих особенности для углов Эйлера не существует общих формул для самых базовых задач с ориентациями, таких как применение одного вращения (ориентации) к другому, расчет разницы между ориентациями и подобных. Поэтому в основном углы Эйлера применяются в пользовательском интерфейсе, но редко используются в математических расчетах.
Axis-angle
Помимо углов Эйлера, любую ориентацию в трехмерном пространстве можно представить в виде вращения вокруг некоторой оси на некоторый угол. В геометрии это доказывается, как теорема вращения Эйлера. В таком представлении ориентация задается двумя величинами:
- Ось вращения (axis) — единичный вектор, определяющий ось вращения.
- Угол поворота (angle или θ) — угол, на который нужно повернуть объект вокруг этой оси.
В Flix ось вращения задается объектом Vector, а угол поворота — числом типа float в радианах:
// Вращение на 45 градусов вокруг оси (1, 2, 3)
Vector axis(1, 2, 3);
float angle = radians(45);
Этот способ более удобен для расчетов, чем углы Эйлера, но все еще не является оптимальным.
Вектор вращения
Если умножить вектор axis на угол поворота θ, то получится вектор вращения (rotation vector). Этот вектор играет важную роль в алгоритмах управления ориентацией летательного аппарата.
Вектор вращения обладает замечательным свойством: если угловые скорости объекта (в собственной системе координат) в каждый момент времени совпадают с компонентами этого вектора, то за единичное время объект придет к заданной этим вектором ориентации. Это свойство позволяет использовать вектор вращения для управления ориентацией объекта посредством управления угловыми скоростями.
Вектора вращения в Flix представляются в виде объектов Vector:
// Вращение на 45 градусов вокруг оси (1, 2, 3)
Vector rotation = radians(45) * Vector(1, 2, 3);
Кватернион
quaternion.h.Вектор вращения удобен, но еще удобнее использовать кватернион. В Flix кватернионы задаются объектами Quaternion из библиотеки quaternion.h. Кватернион состоит из четырех значений: w, x, y, z и рассчитывается из вектора оси вращения (axis) и угла поворота (θ) по формуле:
\[ q = \left( \begin{array}{c} w \\ x \\ y \\ z \end{array} \right) = \left( \begin{array}{c} \cos\left(\frac{\theta}{2}\right) \\ axis_x \cdot \sin\left(\frac{\theta}{2}\right) \\ axis_y \cdot \sin\left(\frac{\theta}{2}\right) \\ axis_z \cdot \sin\left(\frac{\theta}{2}\right) \end{array} \right) \]
На практике оказывается, что именно такое представление наиболее удобно для математических расчетов.
Проиллюстрируем кватернион и описанные выше способы представления ориентации на интерактивной визуализации. Изменяйте угол поворота θ с помощью ползунка (ось вращения константна) и изучите, как меняется ориентация объекта, вектор вращения и кватернион:
Кватернион это наиболее часто используемый способ представления ориентации в алгоритмах. Кроме этого, у кватерниона есть большое значение в теории чисел и алгебре, как у расширения понятия комплексного числа, но рассмотрение этого аспекта выходит за рамки описания работы с вращениями с практической точки зрения.
В прошивке в виде кватернионов представлены, например:
attitude— текущая ориентация квадрокоптера.attitudeTarget— целевая ориентация квадрокоптера.
Операции с кватернионами
Кватернион создается напрямую из четырех его компонент:
// Кватернион, представляющий нулевую (исходную) ориентацию
Quaternion q(1, 0, 0, 0);
Кватернион можно создать из оси вращения и угла поворота, вектора вращения или углов Эйлера:
Quaternion q1 = Quaternion::fromAxisAngle(axis, angle);
Quaternion q2 = Quaternion::fromRotationVector(rotation);
Quaternion q3 = Quaternion::fromEuler(Vector(roll, pitch, yaw));
И наоборот:
q1.toAxisAngle(axis, angle);
Vector rotation = q2.toRotationVector();
Vector euler = q3.toEuler();
Возможно рассчитать вращение между двумя обычными векторами:
Quaternion q = Quaternion::fromBetweenVectors(v1, v2); // в виде кватерниона
Vector rotation = Vector::rotationVectorBetween(v1, v2); // в виде вектора вращения
Шорткаты для работы с углом Эйлера по рысканью (удобно для алгоритмов управления полетом):
float yaw = q.getYaw();
q.setYaw(yaw);
Применения вращений
Чтобы применить вращение, выраженное в кватернионе, к другому кватерниону, в математике используется операция умножения кватернионов. При использовании этой операции, необходимо учитывать, что она не является коммутативной, то есть порядок операндов имеет значение. Формула умножения кватернионов выглядит так:
\[ q_1 \times q_2 = \left( \begin{array}{c} w_1 \\ x_1 \\ y_1 \\ z_1 \end{array} \right) \times \left( \begin{array}{c} w_2 \\ x_2 \\ y_2 \\ z_2 \end{array} \right) = \left( \begin{array}{c} w_1 w_2 - x_1 x_2 - y_1 y_2 - z_1 z_2 \\ w_1 x_2 + x_1 w_2 + y_1 z_2 - z_1 y_2 \\ w_1 y_2 - x_1 z_2 + y_1 w_2 + z_1 x_2 \\ w_1 z_2 + x_1 y_2 - y_1 x_2 + z_1 w_2 \end{array} \right) \]
В библиотеке quaternion.h для этой операции используется статический метод Quaternion::rotate():
// Композиция вращений q1 и q2
Quaternion result = Quaternion::rotate(q1, q2);
Также полезной является операция применения вращения к вектору, которая делается похожим образом:
// Вращение вектора v кватернионом q
Vector result = Quaternion::rotateVector(v, q);
Для расчета разницы между двумя ориентациями используется метод Quaternion::between():
// Расчет вращения от q1 к q2
Quaternion q = Quaternion::between(q1, q2);
Дополнительные материалы
Гироскоп
Поддержание стабильного полета квадрокоптера невозможно без датчиков обратной связи. Важнейший из них — это MEMS-гироскоп. MEMS-гироскоп это микроэлектромеханический аналог классического механического гироскопа.
Механический гироскоп состоит из вращающегося диска, который сохраняет свою ориентацию в пространстве. Благодаря этому эффекту возможно определить ориентацию объекта в пространстве.
В MEMS-гироскопе нет вращающихся частей, и он помещается в крошечную микросхему. Он может измерять только текущую угловую скорость вращения объекта вокруг трех осей: X, Y и Z.
| Механический гироскоп | MEMS-гироскоп |
|---|---|
 |  |
MEMS-гироскоп обычно интегрирован в инерциальный модуль (IMU), в котором также находятся акселерометр и магнитометр. Модуль IMU часто называют 9-осевым датчиком, потому что он измеряет:
- Угловую скорость вращения по трем осям (гироскоп).
- Ускорение по трем осям (акселерометр).
- Магнитное поле по трем осям (магнитометр).
Flix поддерживает следующие модели IMU:
- InvenSense MPU-9250.
- InvenSense MPU-6500.
- InvenSense ICM-20948.
Интерфейс подключения
Большинство модулей IMU подключаются к микроконтроллеру через интерфейсы I²C и SPI. Оба этих интерфейса являются шинами данных, то есть позволяют подключить к одному микроконтроллеру несколько устройств.
Интерфейс I²C использует два провода для передачи данных и тактового сигнала. Выбор устройства для коммуникации происходит при помощи передачи адреса устройства на шину. Разные устройства имеют разные адреса, и микроконтроллер может последовательно общаться с несколькими устройствами.
Интерфейс SPI использует два провода для передачи данных, еще один для тактового сигнала и еще один для выбора устройства. При этом для каждого устройства на шине выделяется отдельный GPIO-пин для выбора. В разных реализациях этот пин называется CS/NCS (Chip Select) или SS (Slave Select). Когда CS-пин устройства активен (напряжение на нем низкое), устройство выбрано для общения.
В полетных контроллерах IMU обычно подключают через SPI, потому что он обеспечивает значительно бо́льшую скорость передачи данных и меньшую задержку. Подключение IMU через интерфейс I²C (например, в случае нехватки пинов микроконтроллера) возможно, но не рекомендуется.
Подключение IMU к микроконтроллеру ESP32 через интерфейс SPI выглядит так:
| Пин платы IMU | Пин ESP32 |
|---|---|
| VCC/3V3 | 3V3 |
| GND | GND |
| SCL | IO18 |
| SDA (MOSI) | IO23 |
| SAO/AD0 (MISO) | IO19 |
| NCS | IO5 |
Кроме того, многие IMU могут «будить» микроконтроллер при наличии новых данных. Для этого используется пин INT, который подключается к любому GPIO-пину микроконтроллера. При такой конфигурации можно использовать прерывания для обработки новых данных с IMU, вместо периодического опроса датчика. Это позволяет снизить нагрузку на микроконтроллер в сложных алгоритмах управления.
Работа с гироскопом
Для взаимодействия с IMU, включая работу с гироскопом, в Flix используется библиотека FlixPeriph. Библиотека устанавливается через менеджер библиотек Arduino IDE:
Чтобы работать с IMU, используется класс, соответствующий модели IMU: MPU9250, MPU6500 или ICM20948. Классы для работы с разными IMU имеют единообразный интерфейс для основных операций, поэтому возможно легко переключаться между разными моделями IMU. Датчик MPU-6500 практически полностью совместим с MPU-9250, поэтому фактически класс MPU9250 поддерживает обе модели.
Ориентация осей гироскопа
Данные с гироскопа представляют собой угловую скорость вокруг трех осей: X, Y и Z. Ориентацию этих осей у IMU InvenSense можно легко определить по небольшой точке в углу чипа. Оси координат и направление вращения для измерений гироскопа обозначены на диаграмме:
Расположение осей координат в популярных платах IMU:
| GY-91 | MPU-92/65 | ICM-20948 |
|---|---|---|
 |  |  |
Магнитометр IMU InvenSense обычно является отдельным устройством, интегрированным в чип, поэтому его оси координат могут отличаться. Библиотека FlixPeriph скрывает это различие и приводит данные с магнитометра к системе координат гироскопа и акселерометра.
Чтение данных
Интерфейс библиотеки FlixPeriph соответствует стилю, принятому в Arduino. Для начала работы с IMU необходимо создать объект соответствующего класса и вызвать метод begin(). В конструктор класса передается интерфейс, по которому подключен IMU (SPI или I²C):
#include <FlixPeriph.h>
#include <SPI.h>
MPU9250 imu(SPI);
void setup() {
Serial.begin(115200);
bool success = imu.begin();
if (!success) {
Serial.println("Failed to initialize the IMU");
}
}
Для однократного считывания данных используется метод read(). Затем данные с гироскопа получаются при помощи метода getGyro(x, y, z). Этот метод записывает в переменные x, y и z угловые скорости вокруг соответствующих осей в радианах в секунду.
Если нужно гарантировать, что будут считаны новые данные, можно использовать метод waitForData(). Этот метод блокирует выполнение программы до тех пор, пока в IMU не появятся новые данные. Метод waitForData() позволяет привязать частоту главного цикла loop к частоте обновления данных IMU. Это удобно для организации главного цикла управления квадрокоптером.
Программа для чтения данных с гироскопа и вывода их в консоль для построения графиков в Serial Plotter выглядит так:
#include <FlixPeriph.h>
#include <SPI.h>
MPU9250 imu(SPI);
void setup() {
Serial.begin(115200);
bool success = imu.begin();
if (!success) {
Serial.println("Failed to initialize the IMU");
}
}
void loop() {
imu.waitForData();
float gx, gy, gz;
imu.getGyro(gx, gy, gz);
Serial.printf("gx:%f gy:%f gz:%f\n", gx, gy, gz);
delay(50); // замедление вывода
}
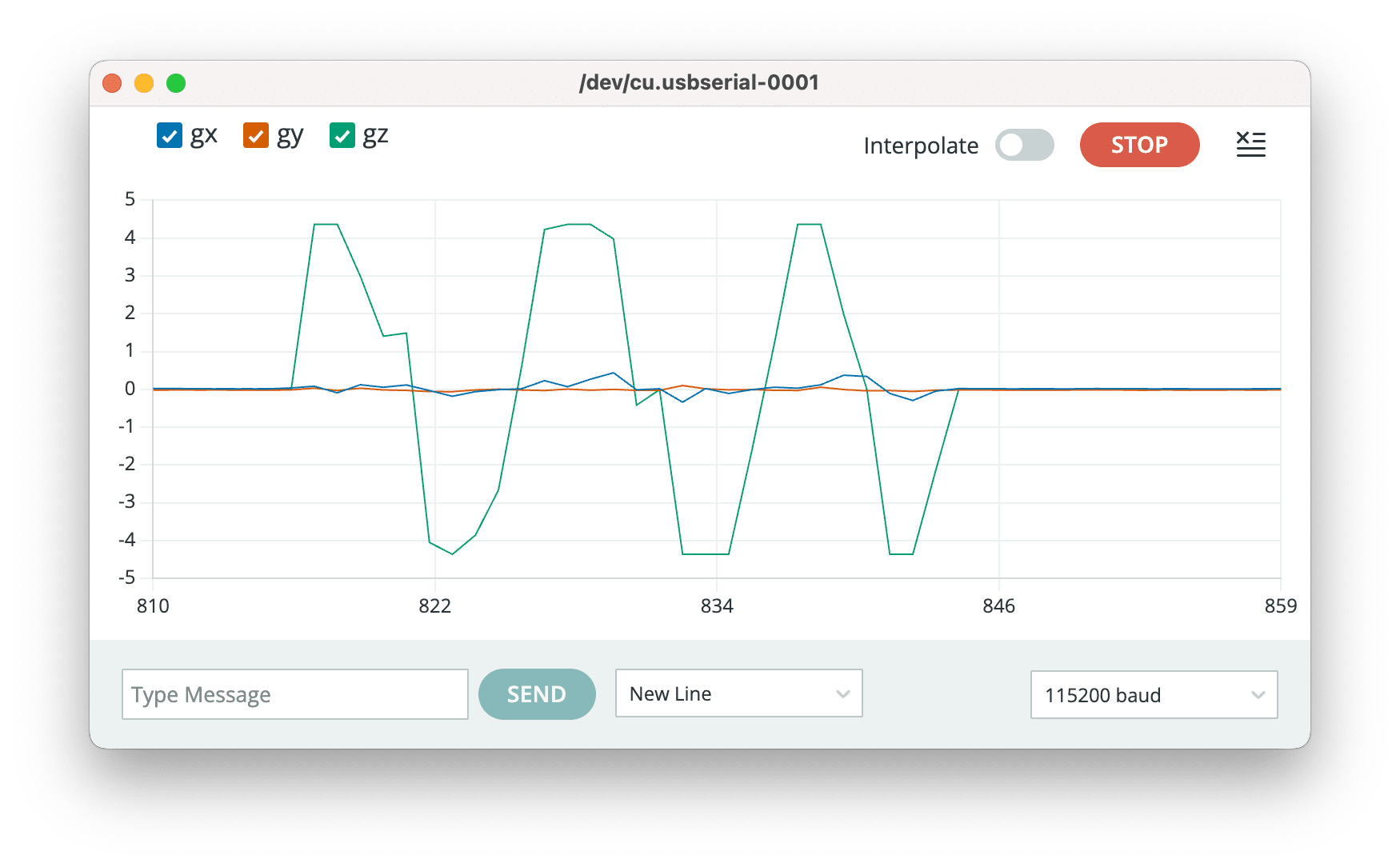
После запуска программы в Serial Plotter можно увидеть графики угловых скоростей. Например, при вращениях IMU вокруг вертикальной оси Z графики будут выглядеть так:
Конфигурация гироскопа
В коде Flix настройка IMU происходит в функции configureIMU. В этой функции настраиваются три основных параметра гироскопа: диапазон измерений, частота сэмплирования и частота LPF-фильтра.
Частота сэмплирования
Большинство IMU могут обновлять данные с разной частотой. В полетных контроллерах обычно используется частота обновления от 500 Гц до 8 кГц. Чем выше частота, тем выше точность управления полетом, но и тем больше нагрузка на микроконтроллер.
Частота сэмплирования устанавливается методом setSampleRate(). В Flix используется частота 1 кГц:
IMU.setRate(IMU.RATE_1KHZ_APPROX);
Поскольку не все поддерживаемые IMU могут работать строго на частоте 1 кГц, в библиотеке FlixPeriph существует возможность приближенной настройки частоты сэмплирования. Например, у IMU ICM-20948 при такой настройке реальная частота сэмплирования будет равна 1125 Гц.
Другие доступные для установки в библиотеке FlixPeriph частоты сэмплирования:
RATE_MIN— минимальная частота для конкретного IMU.RATE_50HZ_APPROX— значение, близкое к 50 Гц.RATE_1KHZ_APPROX— значение, близкое к 1 кГц.RATE_8KHZ_APPROX— значение, близкое к 8 кГц.RATE_MAX— максимальная частота для конкретного IMU.
Диапазон измерений
Большинство MEMS-гироскопов поддерживают несколько диапазонов измерений угловой скорости. Главное преимущество выбора меньшего диапазона — бо́льшая чувствительность. В полетных контроллерах обычно выбирается максимальный диапазон измерений от –2000 до 2000 градусов в секунду, чтобы обеспечить возможность быстрых маневров.
В библиотеке FlixPeriph диапазон измерений гироскопа устанавливается методом setGyroRange():
imu.setGyroRange(imu.GYRO_RANGE_2000DPS);
LPF-фильтр
IMU InvenSense могут фильтровать измерения на аппаратном уровне при помощи фильтра нижних частот (LPF). Flix реализует собственный фильтр для гироскопа, чтобы иметь больше гибкости при поддержке разных IMU. Поэтому для встроенного LPF устанавливается максимальная частота среза:
imu.setDLPF(imu.DLPF_MAX);
Калибровка гироскопа
Как и любое измерительное устройство, гироскоп вносит искажения в измерения. Наиболее простая модель этих искажений делит их на статические смещения (bias) и случайный шум (noise):
\[ gyro_{xyz}=rates_{xyz}+bias_{xyz}+noise \]
Для точной работы подсистемы оценки ориентации и управления дроном необходимо оценить bias гироскопа и учесть его в вычислениях. Для этого при запуске программы производится калибровка гироскопа, которая реализована в функции calibrateGyro(). Эта функция считывает данные с гироскопа в состоянии покоя 1000 раз и усредняет их. Полученные значения считаются bias гироскопа и в дальнейшем вычитаются из измерений.
Программа для вывода данных с гироскопа с калибровкой:
#include <FlixPeriph.h>
#include <SPI.h>
MPU9250 imu(SPI);
float gyroBiasX, gyroBiasY, gyroBiasZ; // bias гироскопа
void setup() {
Serial.begin(115200);
bool success = imu.begin();
if (!success) {
Serial.println("Failed to initialize the IMU");
}
calibrateGyro();
}
void loop() {
float gx, gy, gz;
imu.waitForData();
imu.getGyro(gx, gy, gz);
// Устранение bias гироскопа
gx -= gyroBiasX;
gy -= gyroBiasY;
gz -= gyroBiasZ;
Serial.printf("gx:%f gy:%f gz:%f\n", gx, gy, gz);
delay(50); // замедление вывода
}
void calibrateGyro() {
const int samples = 1000;
Serial.println("Calibrating gyro, stand still");
gyroBiasX = 0;
gyroBiasY = 0;
gyroBiasZ = 0;
// Получение 1000 измерений гироскопа
for (int i = 0; i < samples; i++) {
imu.waitForData();
float gx, gy, gz;
imu.getGyro(gx, gy, gz);
gyroBiasX += gx;
gyroBiasY += gy;
gyroBiasZ += gz;
}
// Усреднение значений
gyroBiasX = gyroBiasX / samples;
gyroBiasY = gyroBiasY / samples;
gyroBiasZ = gyroBiasZ / samples;
Serial.printf("Gyro bias X: %f\n", gyroBiasX);
Serial.printf("Gyro bias Y: %f\n", gyroBiasY);
Serial.printf("Gyro bias Z: %f\n", gyroBiasZ);
}
График данных с гироскопа в состоянии покоя без калибровки. Можно увидеть статическую ошибку каждой из осей:
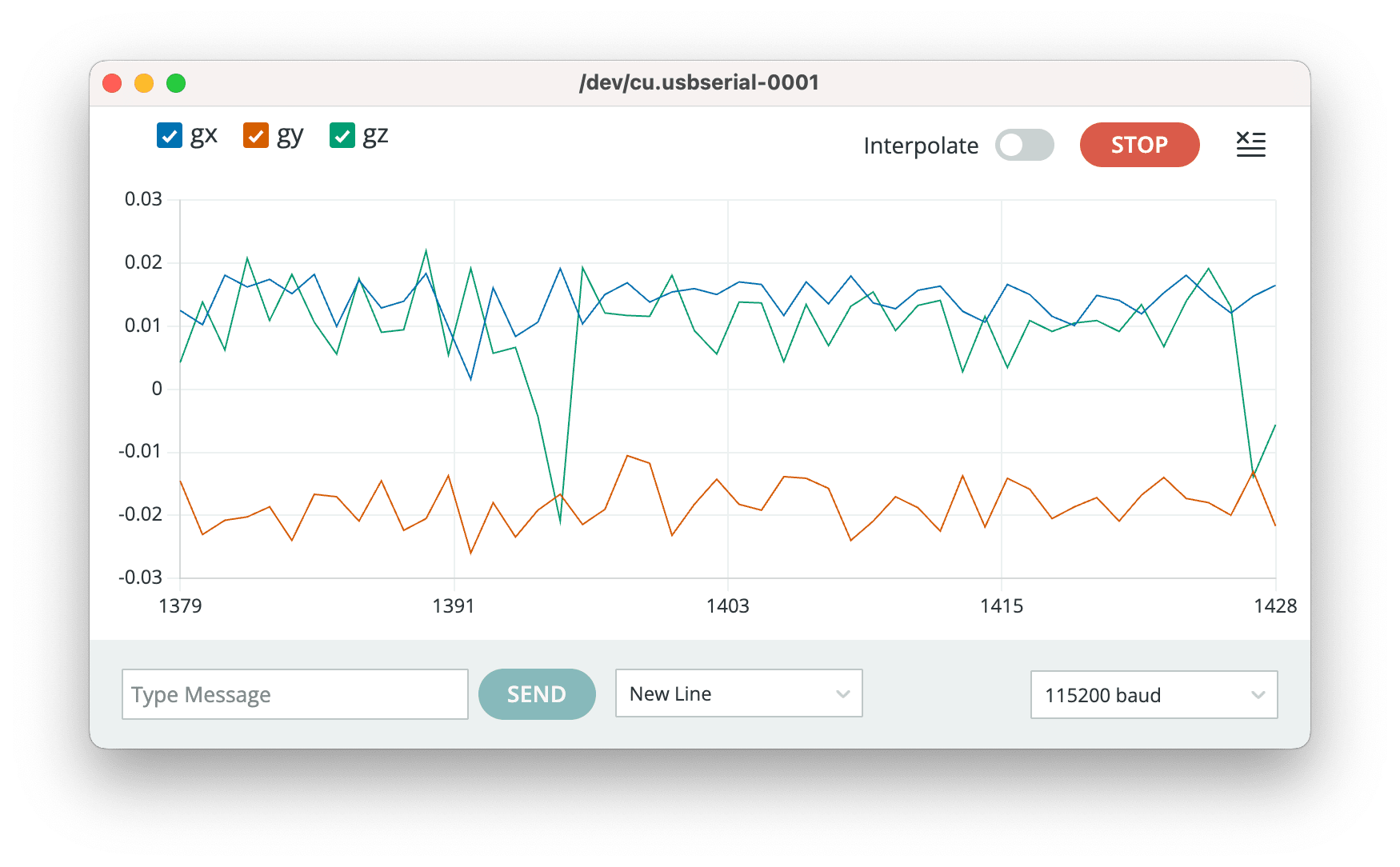
График данных с гироскопа в состоянии покоя после калибровки:
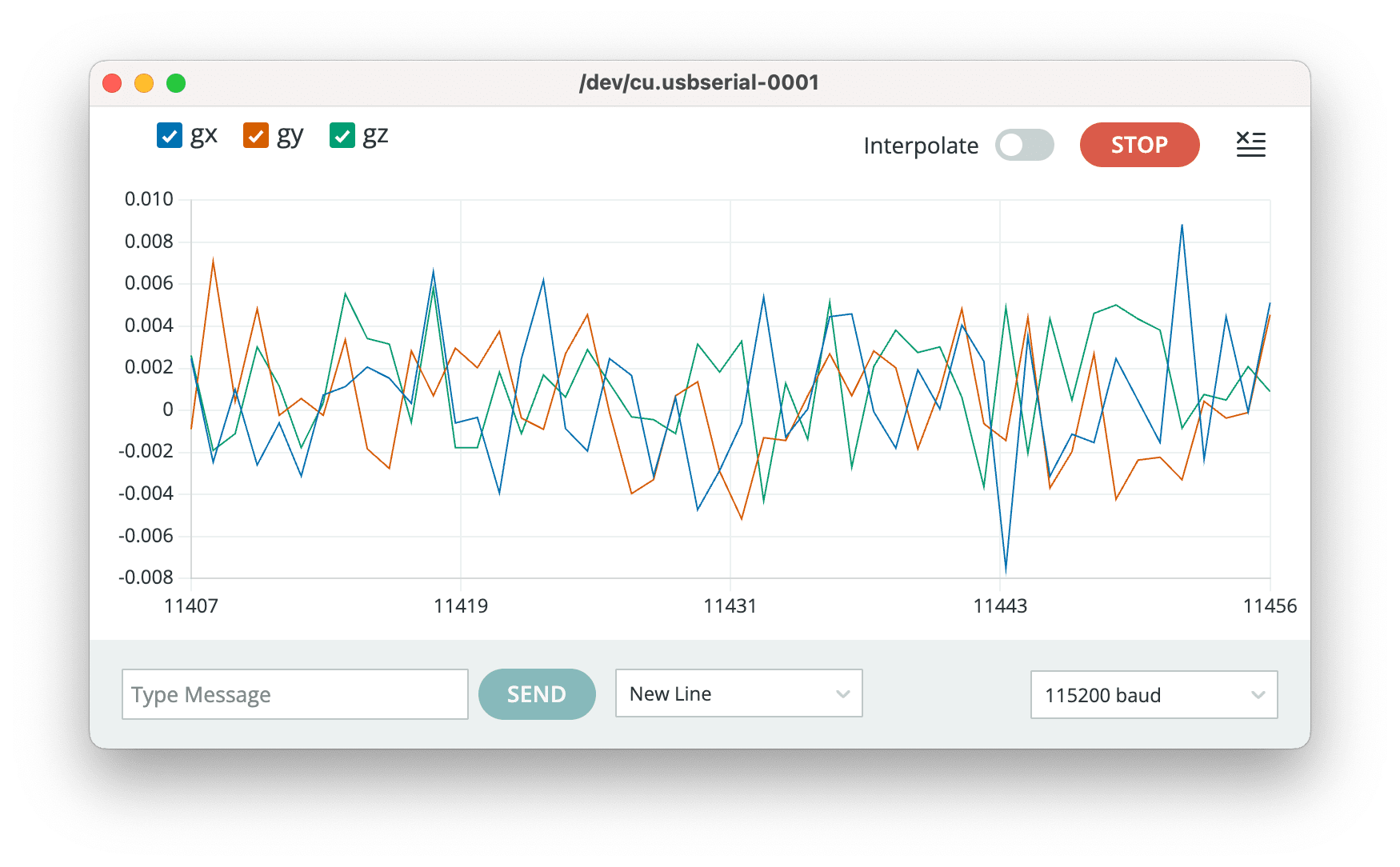
Откалиброванные данные с гироскопа вместе с данными с акселерометра поступают в подсистему оценки состояния.